Теория связи в секретных системах. Часть II.

Способы изображения систем

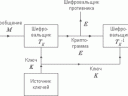
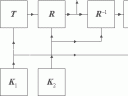
Секретная система, в том виде как она определена выше, может быть изображена различными способами. Один из них (удобный для целей иллюстрации) использует линейные схемы, изображенные на рис. 2. Возможные сообщения представляются точками слева, а возможные криптограммы - точками справа. Если некоторый ключ, скажем, ключ 1, отображает сообщение M₂ в криптограмму Е₂, то M₂ и E₂ соединяются линией, обозначенной значком 1 и т.д..

 

 

Для каждого ключа из каждого сообщения должна выходить ровно одна линия. Если это же верно и для каждой криптограммы, скажем, что система является замкнутой.

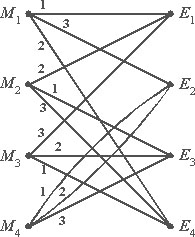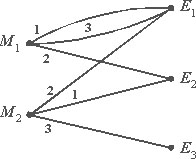Замкнутая система	Незамкнутая система

Более общий способ описания системы состоит в задании операции, с помощью которой, применяя к сообщению произвольный ключ, можно получить криптограмму. Аналогично неявным образом можно определить вероятности различных ключей или с помощью задания способа выбора ключей, или с помощью описания сведений о том, как обычно выбирает ключи противник. Вероятности сообщений определяются просто посредством изложения наших априорных сведений о языке противника, тактической обстановке (которая будет влиять на возможное содержание сообщений) и любой специальной информации, касающейся криптограммы.
В данном разделе рассматриваются несколько примеров шифров. В дальнейшем в целях иллюстрации будем часто ссылаться на эти примеры.

Примеры секретных систем

Шифр простой подстановки.

В таком шифре производится замена каждой буквы сообщения на некоторый определенный символ (обычно также на букву). Таким образом, сообщение

М = m₁m₂m₃m₄...,

где m₁,m₂,... - последовательные буквы, переходит в

E = e₁e₂e₃e₄... = f(m₁)f(m₂)f(m₃)f(m₄)...,

причем функция f(m) имеет обратную функцию. Ключ является просто перестановкой алфавита (если буквы заменяются на буквы), например,

XGUACDTBFHRSLMQVYZWIEJOKNP.

Первая буква - X заменяет букву A, G заменяет B и т.д.

Транспозиция с фиксированным периодом d.

В этом случае сообщение делится на группы символов длины d и к каждой группе применяется одна и та же перестановка. Эта перестановка является ключом; она может быть задана некоторой перестановкой первых d целых чисел.

Таким образом, для d = 5 в качестве перестановки можно взять 23154. Это будет означать, что

m₁m₂m₃m₄m₅m₆m₇m₈m₉m₁₀...

переходит в

m₂m₃m₁m₅m₄m₇m₈m₆m₁₀m₉...

Последовательное применение двух или более транспозиций будет называться составной транспозицией. Если периоды этих транспозиций равны >d₁,...,d_s, то, очевидно, в результате получится транспозиция периода d, где d - наименьшее общее кратное d₁,...,d_s.

Шифр Виженера и его варианты.

В шифре Виженера ключ задается набором из d букв. Такие наборы подписываются с повторением под сообщением и полученные две последовательности складываются по модулю 26 (каждая буква рассматриваемого алфавита нумеруется от А = 0 до Z = 25).

Таким образом,

e_i = m_i+k_i (mod 26),

где k_i - буква ключа, полученная сокращением числа i по модулю d. Например, с помощью ключа GAH получаем

Сообщение	N	O	W	I	S	T	H	E
Повторяемый ключ	G	A	H	G	A	H	G	A
Криптограмма	T	O	D	O	S	A	N	E

Шифр Виженера с периодом 1 называется шифром Цезаря. Он представляет собой простую подстановку, в которой каждая буква сообщения М сдвигается вперед на фиксированное число мест по алфавиту. Это число и является ключом; оно может быть любым от 0 до 25. Так называемый шифр Бофора (Beaufort) и видоизмененный шифр Бофора подобны шифру Виженера. В них сообщения зашифровываются с помощью равенств

e_i = k_i - m_i (mod 26)

и

e_i = m_i - k_i (mod 26)

соответственно. Шифр Бофора с периодом 1 называется обратным шифром Цезаря.

Повторное применение двух или более шифров Виженера будет называться составным шифром Виженера. Он имеет уравнение

e_i = m_i + k_i + l_i + ... + s_i (mod 26),

где k_i,l_i,...,s_i вообще говоря, имеют различные периоды. Период их суммы < >k_i + l_i + ... + s_i, как и в составной транспозиции, будет наименьшим общим кратным отдельных периодов.

Если используется шифр Виженера с неограниченным неповторяющимся ключом, то мы имеем шифр Вернама, в котором

e_i = m_i + k_i (mod 26),

и k_i выбираются случайно и независимо среди чисел 0, 1,..., 25. Если ключом служит текст, имеющий смысл, то имеем шифр "бегущего ключа". Диграммная, триграммная и n-граммнная подстановки.

Вместо подстановки одной буквы можно использовать подстановку диграмм, триграмм и т.д. Для диграммной подстановки в общем виде требуется ключ, состоящий из перестановок 26² диграмм. Он может быть представлен с помощью таблицы, в которой ряд соответствует первой букве диграммы, а столбец - второй букве, причем клетки таблицы заполнены заменяющими символами (обычно также диграммами). Шифр Виженера с перемешанным один раз алфавитом.

Такой шифр представляет собой простую подстановку с последующим применением шифра Виженера

e_i = f(m_i) + k_i,

m_i = f ^-1(e_i - k_i).

"Обратным" к такому шифру является шифр Виженера с последующей простой подстановкой

e_i = g(m_i + k_i),

m_i = g^-1(e_i) - k_i. Матричная система.

Имеется один метод подстановки n-грамм, который заключается в применении к последовательным n-граммам некоторой матрицы, имеющей обратную. Предполагается, что буквы занумерованы от 0 до 25 и рассматриваются как элементы некоторого алгебраического кольца. Если к n-грамме сообщения применить матрицу a_ij то получится n-грамма криптограммы

i = 1,...,n.

Матрица a_ij является ключом, и расшифровка выполняется с помощью обратной матрицы. Обратная матрица будет существовать тогда и только тогда, когда определитель |a_ij| имеет обратный элемент в нашем кольце. Шифр Плэйфер.

Этот шифр является частным видом диграммной подстановки, которая производится с помощью перемешанного алфавита из 25 букв, записанных в виде квадрата 55. (Буква J часто опускается при криптографической работе, так как она редко встречается, и в тех случаях, когда она встречается, ее можно заменить буквой I). Предположим, что ключевой квадрат записывается следующим образом:

L	Z	Q	C	P
A	G	N	O	U
R	D	M	I	F
K	Y	H	V	S
X	B	T	E	W

В этом случае диграмма AC, например, заменяется на пару букв, расположенных в противоположных углах прямоугольника, определяемого буквами A и C, т.е. на LO, причем L взята первой, так как она выше А. Если буквы диграммы расположены на одной горизонтали, то используются стоящие справа от них буквы. Таким образом, RI заменяется на DF, RF заменяется на DR. Если буквы расположены на одной вертикали, то используются буквы, стоящие под ними. Таким образом, PS заменяется на UW. Если обе буквы диграммы совпадают, то можно использовать для их разделения нуль или же одну из букв опустить и т.п.. Перемешивание алфавита с помощью многократной подстановки.

В этом шифре используются последовательно d простых подстановок. Так, если d = 4, то

m₁m₂m₃m₄m₅m₆...

заменяется на

f(m₁)f(m₂)f(m₃)f(m₄)f(m₅)f(m₆)...

и т.д. Шифр с автоключом.

Шифр типа Виженера, в котором или само сообщение или результирующая криптограмма используются в качестве "ключа", называется шифром с автоключом. Шифрование начинается с помощью "первичного ключа" (который является настоящим ключом в нашем смысле) и продолжается с помощью сообщения или криптограммы, смещенной на длину первичного ключа, как в указанном ниже примере, где первичным ключом является набор букв COMET. В качестве "ключа" используется сообщение:

Сообщение

S

E

N

D

S

U

P

P

L

I

E

S

...

Ключ

C

O

M

E

T

S

E

N

D

S

U

P

...

Криптограмма

U

S

Z

H

L

M

T

C

O

A

Y

H

...

Если в качестве "ключа" использовать криптограмму, то получится

Сообщение

S

E

N

D

S

U

P

P

L

I

E

S

...

Ключ

C

O

M

E

T

U

S

Z

H

L

O

H

...

Криптограмма

U

S

Z

H

L

O

H

O

S

T

T

S

...

Дробные шифры.

В этих шифрах каждая буква сначала зашифровывается в две (или более) буквы или в два (или более) числа, затем полученные символы каким-либо способом перемешиваются (например, с помощью транспозиции), после чего их можно снова перевести в первоначальный алфавит. Таким образом, используя в качестве ключа перемешанный 25-буквенный алфавит, можно перевести буквы в двузначные пятеричные числа с помощью таблицы:

	0	1	2	3	4
0	L	Z	Q	C	P
1	A	G	N	O	U
2	R	D	M	I	F
3	K	Y	H	V	S
4	X	B	T	E	W

Например, букве B соответствует число 41₅. После того, как полученный ряд чисел подвергнут некоторой перестановке, его можно снова разбить на пары чисел и перейти к буквам. Коды.

В кодах слова (или иногда слоги) заменяются группами букв. Иногда затем применяется шифр того или иного вида.