Теория связи в секретных системах. Часть III.

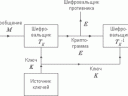
Оценка секретных систем.

Имеется несколько различных критериев, которые можно было бы использовать для оценки качества предлагаемой секретной системы. Рассмотрим наиболее важные из этих критериев.

Количество секретности.

Некоторые секретные системы являются совершенными в том смысле, что положение противника не облегчается в результате перехвата любого количества сообщений.

 

 

Другие системы, хотя и дают противнику некоторую информацию при перехвате очередной криптограммы, но не допускают единственного "решения". Системы, допускающие единственное решение, очень разнообразны как по затрате времени и сил, необходимых для получения этого решения, так и по количеству материала, который необходимо перехватить для получения единственного решения.

Объем ключа.

Ключ должен быть передан из передающего пункта в приемный пункт таким способом, чтобы его нельзя было перехватить. Иногда его нужно запомнить. Поэтому желательно иметь ключ настолько малый, насколько это возможно.

Сложность операции зашифрования и расшифрования.

Операции зашифрования и расшифрования должны быть, конечно, по возможности простыми. Если эти операции производятся вручную, то их сложность приводит к потере времени, появлению ошибок и т.д. Если они производятся механически, то сложность приводит к использованию больших и дорогих устройств.

Разрастание числа ошибок.

В некоторых типах шифров ошибка в одной букве, допущенная при шифровании или передаче, приводит к большому числу ошибок в расшифрованном тексте. Такие ошибки разрастаются в результате операции расшифрования, вызывая значительную потерю информации и часто требуя повторной передачи криптограммы. Естественно, желательно минимизировать это возрастание числа ошибок.

Увеличение объема сообщения.

В некоторых типах секретных систем объем сообщения увеличивается в результате операции шифрования. Этот нежелательный эффект можно наблюдать в системах, в которых делается попытка потопить статистику сообщения в массе добавляемых нулевых символов, или где используются многократные замены. Он имеет место также во многих системах типа "маскировки" (которые не являются обычными секретными системами в смысле нашего определения).

Алгебра секретных систем

Если имеются две секретные системы Т и R, их часто можно комбинировать различными способами для получения новой секретной системы S. Если T и R имеют одну и ту же область (пространство сообщений), то можно образовать своего рода "взвешенную сумму"

S = рТ + qR,

где p + q = 1. Эта операция состоит, во-первых, из предварительного выбора систем T или R с вероятностями p и q. Этот выбор является частью ключа S. После того, как этот выбор сделан, системы T или R применяются в соответствии с их определениями. Полный ключ S должен указывать, какая из систем T или R выбрана и с каким ключом используется выбранная система.

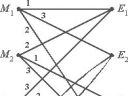
Если Т состоит из отображений Т₁,...,Т_m с вероятностями p₁,...,p_m, a R - из R₁,...,R_k с вероятностями q₁,...,q_k, то система S = рТ + qR состоит из отображений Т₁,...,Т_m,R₁,...,R_k с вероятностями pp₁,...,pp_m,qq₁,...,qq_k соответственно. Обобщая далее, можно образовать сумму нескольких систем

S = p₁Т + p₂R + ... + p_mU, p_i = 1.

Заметим, что любая система T может быть записана как сумма фиксированных операций

T = p₁Т₁ + p₂T₂ + ... + p_mT_m,

где T_i - определенная операция шифрования в системе T, соответствующая выбору ключа i, причем вероятность такого выбора равна p_i.

Второй способ комбинирования двух секретных систем заключается в образовании "произведения", как показано схематически на рис. 3.

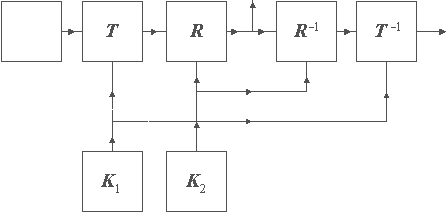
Рис 3. Произведение двух систем S = RT.

Предположим, что T и R - такие две системы, что область определения (пространство языка) системы R может быть отождествлена с областью значения (пространством криптограмм) системы T. Тогда можно применить сначала систему T к нашему языку, а затем систему R к результату этой операции, что дает результирующую операцию S, которую запишем в виде произведения

S = RT.

Ключ системы S состоит как из ключа системы T, так и из ключа системы R, причем предполагается, что эти ключи выбираются соответственно их первоначальным вероятностям и независимо. Таким образом, если m ключей системы T выбирается с вероятностями

p₁,p₂,...,p_m,

а n ключей системы R имеют вероятности

p"₁,p"₂,...,p"_n,

то система S имеет самое большее mn ключей с вероятностями p_ip"_j. Во многих случаях некоторые из отображений R_iT_j будут одинаковыми и могут быть сгруппированы вместе, а их вероятности при этом сложатся.

Произведение шифров используется часто: например, после подстановки применяют перестановку или после перестановки - код Виженера, или же применяют код к тексту и зашифровывают результат с помощью подстановки, перестановки, дробным шифром и т.д.

Можно заметить, что такое умножение, вообще говоря, некоммутативно (т.е. не всегда RS = SR), хотя в частных случаях (таких, как подстановка и перестановка) коммутативность имеет место. Так как наше умножение представляет собой некоторую операцию, оно по определению ассоциативно, т.е. R(ST) = (RS)T = RST. Кроме того, верны законы

p(p"T + q"R) + qS = pp"T + pq"R + qS

(взвешенный ассоциативный закон для сложения);

T(pR + qS) = pTR + qTS
(pR + qS)T = pRT + qST

(право- и левосторонние дистрибутивные законы), а также справедливо равенство

p₁T + p₂T + p₃R = (p₁ + p₂)T + p₃R.

Следует подчеркнуть, что эти операции комбинирования сложения и умножения применяются к секретным системам в целом. Произведение двух систем TR не следует смешивать с произведением отображений в системах T_iR_j, которое также часто используется в настоящей работе. Первое является секретной системой, т.е. множеством отображений с соответствующими вероятностями; второе является фиксированным отображением. Далее, в то время как сумма двух систем pR + qT является системой, сумма двух отображений не определена. Системы T и R могут коммутировать, в то время как конкретные R_j и T_i не коммутируют. Например, если R - система Бофора данного периода, все ключи которой равновероятны, то, вообще говоря,

R_iR_{j =} R_jR_i,

но, конечно, произведение RR не зависит от порядка сомножителей; действительно

RR = V

является системой Виженера того же самого периода со случайным ключом. С другой стороны, если отдельные отображения T_i и R_j двух систем T и R коммутируют, то и системы коммутируют.

Системы, у которых пространства M и E можно отождествить (этот случай является очень частым, если последовательности букв преобразуются в последовательности букв), могут быть названы эндоморфными. Эндоморфная система T может быть возведена в степень Tⁿ.

Секретная система T, произведение которой на саму себя равно T, т.е. такая, что

TT = T,

будет называться идемпотентной. Например, простая подстановка, транспозиция с периодом p, система Виженера с периодом p (все с равновероятными ключами) являются идемпотентными.

Множество всех эндоморфных секретных систем, определенных в фиксированном пространстве сообщений, образует "алгебраическую систему", т.е. некоторый вид алгебры, использующей операции сложения и умножения. Действительно, рассмотренные свойства сложения и умножения можно резюмировать следующим образом:

Множество эндоморфных шифров с одним и тем же пространством сообщений и двумя операциями комбинирования - операцией взвешенного сложения и операцией умножения - образуют линейную ассоциативную алгебру с единицей, с той лишь особенностью, что коэффициенты во взвешенном сложении должны быть неотрицательными, а их сумма должна равняться единице.

Эти операции комбинирования дают способы конструирования многих новых типов секретных систем из определенных данных систем, как это было показано в приведенных примерах. Их можно также использовать для описания ситуации, с которой сталкивается шифровальщик противника, когда он пытается расшифровать криптограмму неизвестного типа. Фактически он расшифровывает секретную систему типа

T = p₁A + p₂B + ... + p_rS + p"X, p_i = 1,

где A,B,...,S в данном случае - известные типы шифров с их априорными вероятностями p_i, а p"X соответствует возможности использования совершенно нового неизвестного шифра.