Струящиеся шёлком бальные наряды, величественные изгибы тяжёлых портьер, "живые" волны покрывал столетиями были предметом заботы художников и модельеров. Но вот американские математики и физики отважилась "поверить алгеброй гармонию". Они получили формулу драпировки.
Группа учёных из Гарварда (Harvard University) потратила не один год, чтобы понять, по каким законам складываются волны на куске ткани, наброшенном на какой-нибудь предмет.
Ведь жёсткость или податливость ткани сильно различается в зависимости от многих факторов.
Как понять, почему вот этот платок, свободно свисающий с шара, даёт 12 волн по окружности, а вот этот — только 10?
А уж если ткань закрывает не шар, а человека — попробуйте-ка предсказать, как она ляжет, да ещё смоделировать движение.
Это, к слову, большая проблема для создателей компьютерных фильмов: трудно сделать колебания складок плащей или вечерних платьев достаточно реалистичными.
 |
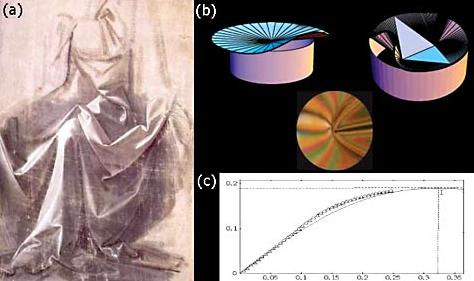 Фрагмент работы гарвардцев — рисунок Леонардо да Винчи и цифровое осмысление законов поведения ткани (иллюстрация с сайта deas.harvard.edu). |
Американцам удалось-таки подступиться к этой проблеме, хотя до полной победы далеко.
Но уже можно посчитать, как поведёт себя закреплённый за один уголок конус ткани, в зависимости от его размеров и свойств материала.
Более того, учёным удалось вывести приблизительные уравнения, которые предсказывают число и форму сгибов в более сложных случаях.
Исследователи обнаружили ряд интересных свойств тканей.
|  | |
 | ||
Любопытно также, что при кажущемся хаосе свободной драпировки, почти весь рельеф можно разделить на простые элементы: плоские участки, цилиндрические и конические перегибы. И лишь в нескольких ключевых точках ткань имеет весьма сложную поверхность.
Пока математики не готовы выдать на-гора программу создания идеального платья. Может быть, это им и не удастся.
Ведь попытки расписать в формулах, как облегает одежда человеческое тело — продолжаются более ста лет.
Когда-то некий парижский математик объявил, что выступит с лекцией: "Математические законы создания идеальной выкройки". Набрался полный зал сгорающих от нетерпения портных.
Но все они дружно встали и ушли после первой фразы докладчика: "Допустим для простоты, что человек имеет форму шара".
Статья получена: Membrana.ru
Противовирусные препараты: за и против
Добро пожаловать в Армению. Знакомство с Арменией
Крыша из сэндвич панелей для индивидуального строительства
Возможно ли отменить договор купли-продажи квартиры, если он был уже подписан
Как выбрать блеск для губ
Чего боятся мужчины
Как побороть страх перед неизвестностью
Газон на участке своими руками
Как правильно стирать шторы
Как просто бросить курить
- 2472 -
